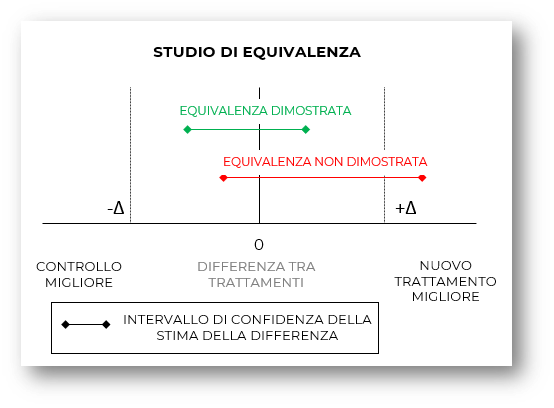
| Studi di bioequivalenza: la maggior parte degli studi con un obiettivo di equivalenza sono studi di bioequivalenza, ovvero studi clinici il cui scopo è quello di confrontare un farmaco generico con il medicinale di riferimento in commercio in modo da dimostrarne la bioequivalenza, ossia l’esser caratterizzati da un profilo di farmacocinetica paragonabile, tramite confronto della biodisponibilità dei due medicinali, ovvero della quantità di medicinale che passa nella circolazione sanguigna dopo somministrazione, in relazione alla velocità con cui questo avviene. Il margine di equivalenza può essere definito come il valore per il quale il paziente non rileverà alcun cambiamento di effetto quando sostituisce un farmaco con l'altro. |
Tornando all’articolo di riferimento di Tandon et al., questo illustra uno studio di superiorità, in quanto l’obiettivo dello studio è quello di verificare se un intervento sullo stile di vita può prevenire il deterioramento dello stato glicemico nelle donne con una recente diagnosi di diabete gestazionale rispetto alla normale pratica clinica.
2) Qual è la variabile primaria?
Come brevemente accennato nel paragrafo precedente, l’obiettivo primario è misurato/quantificato da una variabile primaria. A seconda della scala di misurazione della variabile primaria viene utilizzata una diversa formula per il calcolo della dimensione campionaria.
È necessario specificare “a priori” la variabile primaria:
• Risposta qualitativa:
- variabile dicotomica (ad es. successo/insuccesso) → più semplice da capire e più rilevante clinicamente
- variabile ordinale (più categorie di risposta, ad es. lieve/moderato/severo)
• Risposta quantitativa:
- variabile continua (ad es. Pressione Arteriosa (PA), Volume Espiratorio Massimo nel 1º Secondo (VEMS)) → più efficiente (richiede meno soggetti) ed evita cut-off arbitrari
• Tempo fino all’evento (morte/recidiva):
- ‘cosiddetti’ dati di sopravvivenza (ad es. Overall Survival (OS), Progression-Free Survival (PFS))
Nell’articolo di riferimento che stiamo analizzando, la variabile primaria dello studio considerata per il calcolo del sample size è il peggioramento dello stato glicemico (variabile dicotomica): il dimensionamento si è basato su un test χ2 che confrontava le proporzioni a 24 mesi (13% vs 20%).
3) Qual è la variabilità della variabile primaria?
Un elemento presente nel calcolo della dimensione del campione è la variabilità della variabile primaria, spesso identificata con la deviazione standard. Questa è una misura della dispersione dei dati in una popolazione specifica. Può essere ottenuta esaminando la letteratura pubblicata o a partire da studi pilota, anche se quest’ultima opzione non è sempre percorribile. Qualora non fosse possibile ricavare la variabilità/dispersione dei risultati, è necessario ipotizzare una stima e ricorrere a simulazioni.
Ovviamente, dovendo specificare delle assunzioni “a priori”, ci sono forti margini di incertezza riguardo ai valori ipotizzati che dovranno poi essere controllati a fine studio sulla base dei dati realmente osservati.
Maggiore è la variabilità della variabile primaria, maggiore sarà la dimensione del campione richiesta per lo studio.
Nell’articolo di riferimento di Tandon et al., la variabile primaria dello studio considerata per il calcolo del sample size è il peggioramento dello stato glicemico: essendo una variabile dicotomica non è stata (correttamente) considerata la deviazione standard.
4) Qual è la minima differenza fra trattamenti clinicamente significativa?
L’elemento più critico, ma anche maggiormente rilevante, nel dimensionamento campionario consiste nel quantificare/ipotizzare l’effetto che ci si attende con il nuovo trattamento sperimentale rispetto all’effetto atteso con il trattamento di controllo.
Questo si traduce nel definire la minima differenza tra trattamenti considerata clinicamente significativa, ovvero la più piccola differenza tra trattamenti considerata clinicamente rilevante nella gestione dei pazienti, oppure la differenza che gli sperimentatori dello studio considerano essere sia biologicamente plausibile sia rilevante da un punto di vista clinico.
La stima di tale differenza tra i due trattamenti in studio può derivare da studi precedenti: per il trattamento sperimentale da studi pilota o dossier registrativi, per il trattamento di controllo da precedenti studi a confronto con placebo (sostanza inerte o trattamento medico senza alcuna proprietà terapeutica) o anche da meta-analisi pubblicate.
Maggiore è l'effetto di un trattamento sperimentale rispetto ad un trattamento di controllo (cioè, maggiore è la differenza negli esiti dei trattamenti da dimostrare), minore sarà il numero di soggetti necessari per dimostrare tale effetto. Viceversa, più piccolo è l'effetto (ma comunque clinicamente rilevante), maggiore sarà la dimensione del campione richiesta per dimostrare tale differenza. Per questo motivo, gli studi in cui il gruppo di controllo è costituito dal placebo richiedono in genere meno pazienti di quelli in cui il gruppo di controllo è un trattamento attivo, poiché ci si aspetta una differenza maggiore di un farmaco sperimentale vs. placebo (in quanto l’effetto in questo gruppo dovrebbe essere nullo).
Analogamente alla stima della variabilità della variabile primaria, anche per la stima della differenza attesa tra trattamenti (minima differenza clinicamente significativa) esistono dei margini d’incertezza dovendola definire “a priori”.
Nell’articolo di Tandon et al., a questo proposito, è stata ipotizzata una riduzione relativa del 35% del peggioramento dello stato glicemico, assumendo un'incidenza cumulativa del 20% nel gruppo di controllo. Questo si traduce in un'incidenza cumulativa del 13% nel gruppo sperimentale.
5) Quale rischio di errore siamo disposti a correre nel valutare tale differenza?
Errore di Tipo I (alpha)
L’errore di Tipo I (α), denominato anche livello di significatività, misura la probabilità di rifiutare l'ipotesi nulla quando in realtà questa è vera (ovvero di concludere che la differenza tra due trattamenti è statisticamente significativa quando non lo è). In altre parole, l’errore di Tipo I si riferisce ai risultati falsi positivi.
Solitamente il livello α è prefissato a 0,05 (o 0,01), il che significa che è tollerabile avere una probabilità del 5% (o 1%) di rifiutare erroneamente l'ipotesi nulla. Minore è l'errore alfa, quindi più bassa è la probabilità di concludere erroneamente, maggiore sarà la dimensione del campione richiesta.
Errore di Tipo II (beta)
L’errore di Tipo II (β) misura la probabilità di accettare l'ipotesi nulla quando in realtà questa è falsa (ovvero di concludere che non c’è differenza tra due trattamenti, o quest’ultima è pari a 0, quando in realtà i due trattamenti sono differenti). In altre parole, l’errore di Tipo II si riferisce ai risultati falsi negativi.
Solitamente il livello β è prefissato a 0,20 (o 0,10), il che significa che è tollerabile avere una probabilità del 20% (o 10%) di ottenere un falso negativo.
Potenza
La potenza è il complemento a uno dell’errore di Tipo II (ovvero 1-β) e rappresenta la probabilità desiderata di osservare la differenza attesa tra due trattamenti, se vera, al livello di significatività α (cioè la probabilità di rifiutare correttamente l'ipotesi nulla quando è falsa).
Solitamente la potenza è prefissata pari all’80% (o 90%), il che significa che la probabilità di rifiutare correttamente un'ipotesi nulla è almeno dell'80% (o 90%). Maggiore è la potenza, maggiore sarà la dimensione del campione richiesta.
|
Tipo I (α) < Tipo II (β): se il controllo è già ampiamente utilizzato ed è noto per essere ragionevolmente sicuro ed efficace, mentre il trattamento sperimentale è nuovo, costoso e potrebbe produrre gravi effetti collaterali.
Tipo I (α) > Tipo II (β): se non esiste un trattamento di controllo comprovato e il trattamento sperimentale è relativamente poco costoso, facile da usare e non è noto per avere effetti collaterali gravi.
Tipo I (α) = Tipo II (β): se entrambi i trattamenti (sperimentale e di controllo) sono nuovi, circa uguali in termini di costi, e ci sono buone ragioni per considerarli entrambi relativamente sicuri.
|
Nell’articolo di Tandon et al. in esame, l’errore di Tipo I per lo studio in oggetto era stato fissato al 5% e l’errore di Tipo II al 10% (ovvero una potenza del 90%). Durante lo studio gli autori hanno deciso di modificare l’analisi primaria (analisi statistica dell’endpoint primario) per problemi legati al tempo di arruolamento, pertanto hanno ricalcolato la potenza del test usato per l’analisi principale con il numero di soggetti effettivamente arruolati nello studio, concludendo di avere una potenza pari all’80%.
6) Qual è la percentuale attesa di drop-out?
Un ultimo elemento da tenere in considerazione per la stima della dimensione campionaria è la percentuale attesa di drop-out. Non bisogna dimenticare infatti che il numero che si ottiene dal calcolo della dimensione del campione rappresenta il numero necessario di soggetti validi per l’analisi primaria, e non dei soggetti che iniziano lo studio. Pertanto, la numerosità campionaria deve essere aggiustata per la percentuale attesa di drop-out, ovvero per la percentuale di soggetti che ci si attende che non arrivino a completare lo studio (per diversi motivi).





